Towards Proactive Value Alignment

Figure 1: An agent proactively queries a human user for alignment (generated by GPT-4o).

TL;DR

Language models aligned via reinforcement learning from human feedback (RLHF) generally behave helpfully, but often fail to adapt to individual users. To improve user-specific alignment, language models need to proactively and efficiently elicit individual user preferences.

We frame this as a query selection problem and use Expected Value of Information (EVOI) as the objective, which quantifies how much a user response may improve the agent’s decisions. While computing EVOI is often computationally intractable, we discuss approximations and explore how it can be applied to language models.

Reinforcement learning from human feedback (RLHF) (Ouyang et al., 2022) successfully aligns language models with general human values, such as honesty, helpfulness, and harmlessness. When you give it an instruction, it usually responds in a polite and professional way. If you add more context, it thanks for the additional information and gives you a presumably better response.

However, interacting with a language model may feel different from talking to a real person. If you ask a friend who is knowledgeable about a topic, they will try to understand your intent and your background knowledge on the topic. They may ask clarifying questions and explain things in a way that you can understand. These proactive traits are often missing in today’s language models.

Most existing RLHF works focus on general value alignment, which aligns language models to general human values. There should be a second, crucial phase of alignment, which we call user-specific alignment. In this phase, the language model needs to be aligned to the individual user’s preferences.

The user-specific alignment phase may have the following aspects:

• Knowing relevant facts about the user. The language model should know some background knowledge of the user that can help better answer the user’s question or follow the instructions. For example, ChatGPT uses memory (and the newly-announced improved memory) to store facts about the user and retrieve related information in future conversations.
• Knowing preferred styles of model responses. The language model should know the user’s preferences and adapt its response accordingly. For example, ChatGPT supports custom instructions that allows the user to specify their preferred styles of model responses.

While language models can passively collect facts or preferences from the users, this may not be efficient. In this post, we explore how language models can proactively align with users — how to ask, adapt, and care to know the user’s preferences.

Note that the goal of this post is not to deliver new results, but to gain inspiration from classical reinforcement learning literature for improving language model alignment. We will see how concepts like reward uncertainty and query selection can inform the design of more proactive language models.

1. Background: Reward-Uncertain Markov Decision Processes

We assume that the reader is already familiar with the concept of Markov decision process (MDP) (Sutton & Barto, 2018), including states, actions, transitions, and reward functions.

In classical RL, the reward function $r$ is typically known to the agent, which is expected in domains such as video games and board games (Silver et al., 2016) (Schrittwieser et al., 2020). However, in many other more realistic or complex domains, like a language model interacting with a human user, the agent may be uncertain about the reward function.

When the agent is uncertain about the reward function, we can model the environment as a reward-uncertain MDP. We need to define the following components (adapted from Ramachandran & Amir (2007)):

• $\tau$ (tau) is a trajectory. In the context of language models, it’s the response generated by the model.
  • Example: $\tau = \text{“The capital of France is Paris.”}$
• $r$ is a reward function.
  • Example: $r_F$ is a reward function that prefers formal responses, and $r_E$ is a reward function that prefers engaging responses.
• $V^\tau_r$ is the value of a trajectory $\tau$ under reward function $r$.
  • Example: $V^\tau_{r_F} = 1$ if $\tau$ is formal, and $V^\tau_{r_F} = 0$ otherwise; $V^\tau_{r_E} = 1$ if $\tau$ is engaging, and $V^\tau_{r_E} = 0$ otherwise.
• $R$ is a space of reward functions, which is assumed to contain the true reward function, denoted as $r^*$, that best aligns with the user’s preferences. For simplicity, we assume $R$ is finite in this post.
  • Example: $R = \{r_F, r_E\}$.
• $\psi$ is the agent’s prior belief over the reward functions. We denote by $P(r; \psi)$ the probability that $r$ is the true reward function under the prior belief $\psi$.
  • Example: $P(r_F; \psi) = P(r_E; \psi) = 0.5$ when the agent has a uniform prior over the reward functions.

Clearly, if the agent is certain about the true reward function, $r^*$, it can find the optimal trajectory under the reward function: $V^*_\psi = \arg\max_{\tau} V^\tau_{r^*}$. However, the challenge is that the true reward function is unknown to the agent.

Notes on Notation:

• We consider deterministic policies and do not consider sampling from a random policy. So instead of defining policies, we only define trajectories.
• Note that $\psi$ is a distribution, not a random variable. So we use $P(r; \psi)$ instead of $P(r \mid \psi)$.

Finding the Optimal Trajectory Under Reward Uncertainty. Although we do not focus on how to efficiently find the optimal policy / trajectory under reward uncertainty, it’s worth pointing out that the optimal trajectory under reward uncertainty is the same as the optimal trajectory under the mean reward function (adapted from Theorem 3 in Ramachandran & Amir (2007)):

\[\begin{equation} V^*_\psi = \max_{\tau} \mathbb{E}_{r \sim \psi} \left[ V^\tau_r \right] \\ = \max_{\tau} \left[ V^\tau_{\bar{r}_\psi} \right], \label{eq:optimal-trajectory-under-uncertainty} \end{equation}\]

where $\bar{r}_\psi(s, a) = \sum_{r \in R} P(r; \psi) \cdot r(s, a)$ is the mean reward function. So under reward uncertainty, we can still find the optimal trajectory in the same way as finding the optimal trajectory for a known reward function.

1.1 Inferring the Reward Function

Since the agent is uncertain about the reward function, it requires extra data to help infer the true reward function. There are two common ways to infer the reward function: learning from demonstrations and learning from feedback.

In learning from demonstrations, the agent infers a reward function from expert trajectories provided by a human user. To achieve this, there are well-known algorithms like inverse reinforcement learning (IRL) (Ng & Russell, 2000), maximum entropy IRL (Ziebart et al., 2008), and Bayesian IRL (Ramachandran & Amir, 2007).

In learning from feedback, the agent generates trajectories and observes the human user’s feedback on them. This is the idea behind TAMER (Knox & Stone, 2009) and preference-based RL (Christiano et al., 2017). Clearly, this requires less effort from the human user – the human user does not need to provide trajectories, but only feedback on them. So, this is more scalable and is the setting commonly used in RLHF.

2. Proactive Querying in Classical RL

To efficiently elicit more informative feedback and improve alignment, the agent must proactively select useful queries. In this section, we dive into the learning from feedback literature.

We first define the querying process between the agent and the human user. We then review two common methods for query selection: entropy-based query selection and Expected Value of Information (EVOI).

2.1 The Querying Process

Figure 2: The querying process between the agent and the human user. The agent selects a query, receives the user's response, and updates its reward belief accordingly.

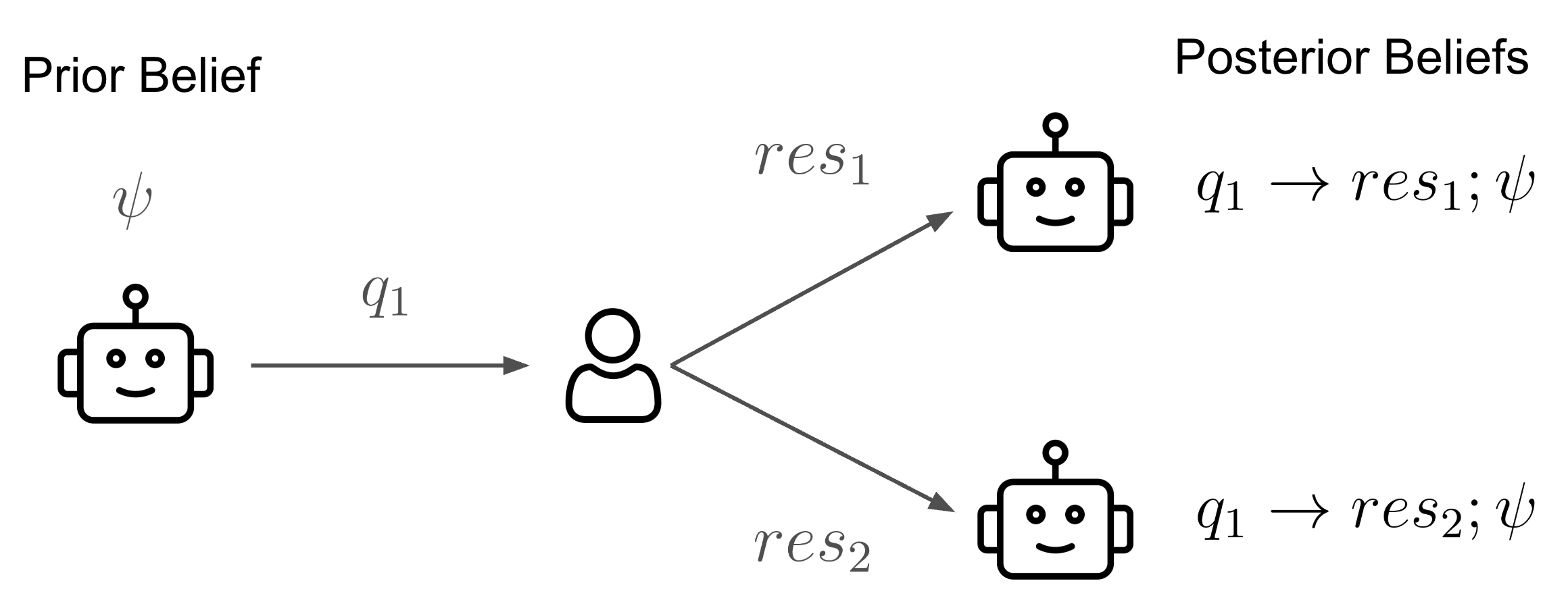
We consider a querying process in which the agent interacts with the user to refine its belief over reward functions:

• Step 0: Prior belief. The agent has a prior belief $\psi$ over the reward functions.
• Step 1: Query selection. The agent selects a query $q$ to ask the human user.
• Step 2: Receiving human response. The human user responds with a response $res$.
• Step 3: Belief update. The agent updates its belief $\psi$ over the reward functions based on the response, and obtains the posterior belief.
• Step 4: Optimizing posterior trajectory. The agent finds the optimal trajectory under the updated belief.

Let’s break down the querying process step by step. The process is illustrated in Figure 2.

Step 0: Prior belief. Initially:

• The agent knows a space of possible reward functions $R$ (which contains the true reward function $r^*$) and a prior belief $\psi$ over them.
• The human user knows the true reward function $r^*$.

For example, suppose the agent is assisting a user with text generation. The reward function could be one of $r_F$, which prefers formal, accurate completions, and $r_E$, which prefers engaging, entertaining completions.

The agent does not know which reward function best aligns with the user’s preferences, and it maintains a belief $\psi$ over these candidates.

Step 1: Query selection. To gain more information about the user’s preferences, the agent can choose to pose a query. For example, the agent can ask:

$q = \text{“Do you prefer formal answers or fun, engaging ones?”}$

Step 2: Receiving human response. Given this query, the human user may respond with one of the possible responses given their preferences. For example:

• If the user prefers formality ($r^* = r_F$), they might respond with $res_F = \text{“I prefer formal answers.”}$
• If they prefer engagement ($r^* = r_E$), they might say $res_E = \text{“I like engaging responses.”}$

Step 3: Belief update. After receiving the response, the agent updates its belief $\psi$ accordingly – placing higher probability on the reward function that better explains the user’s answer.

In our example, if the user responds with $res_F = \text{“I prefer formal answers.”}$, the agent would update its belief to increase the probability of $r_F$ and decrease the probability of $r_E$. Similarly, if the response is $res_E = \text{“I like engaging responses.”}$, the belief would shift in favor of $r_E$.

Formally, given a query $q$ and a response $res$, we denote the posterior belief as $q \rightarrow res; \psi$, following the notation in Zhang et al. (2017). This belief update simply follows the Bayes’ rule:

\[\begin{equation} P(r; [q \rightarrow res; \psi]) \propto P(q \rightarrow res; r) \cdot P(r; \psi). \label{eq:bayes-update} \end{equation}\]

In this equation:

• $P(r; [q \rightarrow res; \psi])$ is the probability that $r$ is the true reward function under the posterior belief $q \rightarrow res; \psi$.
• $P(q \rightarrow res; r)$ is the query response model, which is the probability that the user responds $res$ to $q$ given the reward function $r$. One commonly-used response model in RLHF is the Bradley–Terry model.

Step 4: Optimizing posterior trajectory. The agent finds the optimal trajectory under the updated belief, using Equation \ref{eq:optimal-trajectory-under-uncertainty} (replacing $\psi$ with the posterior belief $q \rightarrow res; \psi$).

In our example, if after the belief update the agent is highly confident that $r_F$ is the true reward function, it would generate formal, accurate text completions. Conversely, if it believes $r_E$ is more likely, it would focus on creating engaging and entertaining content.

2.2 Entropy-based Query Selection

How should the agent select queries to elicit more informative feedback? One way is to choose queries that reduce the agent’s uncertainty over the reward functions. This can be measured by entropy, which is commonly used in the reinforcement learning and language model literature (Liang et al., 2022) (Piriyakulkij et al., 2023):

\[\begin{equation} H(\psi) = - \sum_{r \in R} P(r; \psi) \log P(r; \psi). \label{eq:entropy} \end{equation}\]

A lower entropy indicates higher certainty about the user’s true reward function.

To determine how a query $q$ reduces the uncertainty, the agent computes the posterior belief $q \rightarrow res; \psi$ for all possible responses $res$, and computes the expected entropy:

\[\begin{equation} \sum_{res} P(q \rightarrow res; \psi) \cdot H(q \rightarrow res; \psi), \label{eq:posterior-entropy} \end{equation}\]

where $P(q \rightarrow res; \psi)$ is the probability of the response $res$ given the query $q$ and the prior belief $\psi$, which simply marginalizes over the reward functions in $R$:

\[\begin{equation} P(q \rightarrow res; \psi) = \sum_{r \in R} P(q \rightarrow res; r) \cdot P(r; \psi). \label{eq:query-response-probability} \end{equation}\]

The agent’s objective is to choose a query $q$ that minimizes Equation \ref{eq:posterior-entropy}.

This objective intuitively makes sense – it’s always better to be more certain about the true reward function. However, entropy minimization does not take into account whether the received query response will actually lead to better decisions. It is possible that a query reduces uncertainty but does not lead to a better trajectory.

In the next section, we introduce Expected Value of Information (EVOI), which directly optimizes for improved behavior.

2.3 Expected Value of Information (EVOI)

To quantify how much better the agent’s decision becomes after asking a query, we consider Expected Value of Information (EVOI) (Viappiani & Boutilier, 2010), defined as below.

Given a prior $\psi$ over reward functions $R$, the EVOI of a query $q$ is:

\[\begin{equation} EVOI(q, \psi) = \sum_{res} P(q \rightarrow res; \psi) \left[ V^*_{q \rightarrow res; \psi} \right] - V^*_\psi, \label{eq:evoi} \end{equation}\]

where

• $V^*_\psi$ is the value of the optimal trajectory under the prior belief;
• $V^*_{q \rightarrow res; \psi}$ is the value of the optimal trajectory under the posterior belief $q \rightarrow res; \psi$;
• $P(q \rightarrow res; \psi)$ is the probability of the response $res$ given the query $q$ and the prior belief $\psi$. This is computed using Equation \ref{eq:query-response-probability}.

Intuitively, EVOI measures the expected increase in the value of the optimal trajectory after posing a query. If the agent’s optimal trajectory does not change regardless of the user’s answer, then EVOI is zero—even if the agent reduces its uncertainty about the reward function. On the other hand, if a query leads the agent to choose a better trajectory in some cases, EVOI will be positive. This makes EVOI a more useful criterion when the goal is to improve behavior, not just learn the true reward function $r^*$.

Below we show an example of finding queries using entropy and EVOI, and show that EVOI helps find a more useful query.

Example of Finding Queries Using Entropy and EVOI

Suppose the agent chooses between two trajectories $\tau_1$ and $\tau_2$, and the reward function is one of:

Reward Function	$V^{\tau_1}_r$	$V^{\tau_2}_r$
$r=r_1$	1.0	0.0
$r=r_2$	0.0	1.0
$r=r_3$	0.5	0.5

Let the prior be uniform: $P(r_1; \psi) = P(r_2; \psi) = P(r_3; \psi) = \frac{1}{3}$. For simplicity and with a slight abuse of notation, we will abbreviate this as $\psi = [\frac{1}{3}, \frac{1}{3}, \frac{1}{3}]$ in this example, where $\psi_i = P(r_i; \psi)$.

The expected values of the two trajectories are:

• $V^{\tau_1}_\psi = \frac{1}{3}(1.0 + 0.0 + 0.5) = 0.5$
• $V^{\tau_2}_\psi = \frac{1}{3}(0.0 + 1.0 + 0.5) = 0.5$

Hence, under the prior, the agent is indifferent between the two trajectories: $V^*_\psi = 0.5$.

Now consider two queries:

• Query $q_1$, with two possible responses with the following posterior beliefs:

  • $res^{(1)}_1$: posterior $[q_1 \rightarrow res^{(1)}_1; \psi] = [1.0, 0.0, 0.0]$
  • $res^{(1)}_2$: posterior $[q_1 \rightarrow res^{(1)}_2; \psi] = [0.0, 0.5, 0.5]$

• Query $q_2$, with two possible responses with the following posterior beliefs:

  • $res^{(2)}_1$: posterior $[q_2 \rightarrow res^{(2)}_1; \psi] = [0.5, 0.5, 0.0]$
  • $res^{(2)}_2$: posterior $[q_2 \rightarrow res^{(2)}_2; \psi] = [0.0, 0.0, 1.0]$

Entropy-based Query Selection. Both queries reduce uncertainty to the same extent (with probability $\frac{1}{3}$, it’s certain about the true reward function; with probability $\frac{2}{3}$, it’s uniformly uncertain about two reward functions). So their expected entropy are the same. The entropy-based selection is indifferent between $q_1$ and $q_2$.

EVOI-based Query Selection. Let’s analyze the EVOI of $q_1$ and $q_2$.

• Under $q_1$,
  • If the response is $res^{(1)}_1$, then $r_1$ is the true reward function, and the agent chooses $\tau_1$, which is optimal under $r_1$.
  • If the response is $res^{(1)}_2$, then $r_2$ or $r_3$ is the true reward function, and the agent chooses $\tau_2$, which is better than $\tau_1$ in expectation.
• Under $q_2$,
  • If the response is $res^{(2)}_1$, then $r_1$ or $r_2$ is the true reward function, and the agent remains indifferent between $\tau_1$ and $\tau_2$.
  • If the response is $res^{(2)}_2$, then $r_3$ is the true reward function, and the agent remains indifferent between $\tau_1$ and $\tau_2$.

So the EVOI of $q_1$ is higher than $q_2$.

In summary, EVOI prefers $q_1$ because it leads to a better trajectory, whereas $q_2$ never changes the agent’s choice. This illustrates that EVOI selects more helpful queries than the entropy-based objective.

2.4 Challenges and Limitations of EVOI

Computational Cost. A major challenge with EVOI is its computational cost. Practically, the agent needs to:

• Sample a set of queries.
• For each query, consider all of its possible responses.
• For each possible response, compute the posterior belief over the reward functions, and then find the optimal trajectory under the updated belief.
  • In reality, the agent needs to run an RL algorithm to find the posterior optimal policy / trajectory under the posterior belief.

This is clearly not scalable considering that we need to run an RL algorithm for each possible posterior belief. Zhang et al. (2017) (disclaimer: my own work) show that we can find a provably approximately optimal query by converting the query selection as a combinatorial optimization problem. However, it makes the assumption that the state space, the action space, and the reward function candidates ($R$) are finite. So it remains a challenge to efficiently find EVOI-optimal queries in a general setting.

Assumptions on the Reward Function Space. Our framework assumes we have access to the reward function space $R$ and prior beliefs $\psi$. In practice, these are rarely known a priori. One potential solution is to leverage language models to estimate these components – for example, by prompting the model to enumerate possible user preferences based on the given instruction.

Finding the Optimal Sequence of Queries is Even More Challenging. So far, we’ve considered selecting a single query. However, alignment often requires a sequence of queries. Planning such a sequence involves lookahead — the agent must reason about future responses, belief updates, and long-term gains. This greatly increases the complexity and makes query selection a sequential decision-making problem (Cohn et al., 2014).

3. Proactive Querying in Language Models

We have reviewed how to proactively query to improve the agent’s policy in a classical RL setting. Now let’s review how querying is done in language models in the literature.

3.1 Proactive Querying During Inference

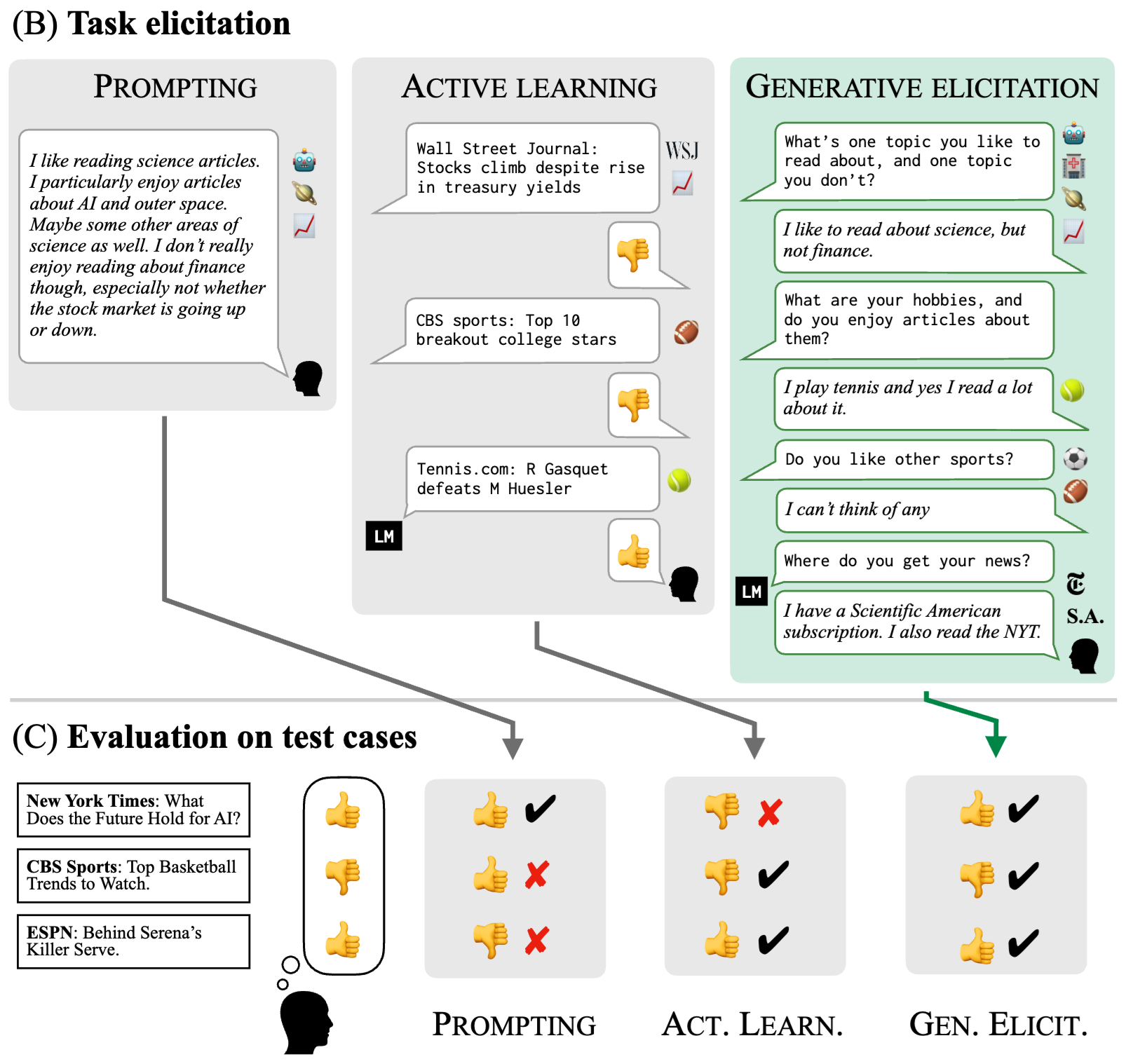
Kuhn et al. (2023) propose CLAM (Selective Clarification for Ambiguous Questions), which aims to improve language models’ ability to handle ambiguous user queries. The approach involves training the model to identify when a user’s question is ambiguous and selectively generate clarification questions to resolve the ambiguity. The authors demonstrate that CLAM improves to higher user satisfaction and task success rates.

Li et al. (2023) similarly allow language models to generate clarification questions when user instructions are ambiguous. Given an input with multiple plausible completions, each optimal under a different latent preference, the model is trained to produce a question whose answer would disambiguate the user’s intent. This method treats clarification as a two-stage process — ask, then act — and integrates question generation into the standard decoding pipeline. Experiments show that it improves task accuracy and user satisfaction compared to directly responding without clarification.

Figure 3: Synthesized queries using language models to elicit the user's preferences. (Li et al., 2023)

3.2 Proactive Querying During Training

Hong et al. (2023) propose a framework for zero-shot goal-directed dialogue by training agents on imagined conversations. An imagination engine generates synthetic dialogs between humans and a suboptimal agent. These imagined conversations are used to train a downstream RL agent that learns to ask questions, elicit preferences, and make progress toward task goals. The agent evaluates full conversation trajectories and improves its policy through reinforcement learning, without requiring access to real human users during training.

Figure 4: An imagined dataset of dialogues between humans and a potentially suboptimal agent is synthesized by the imagination engine, then used to train a downstream RL agent. Blue boxes indicate handcrafted quantities. (Hong et al., 2023)

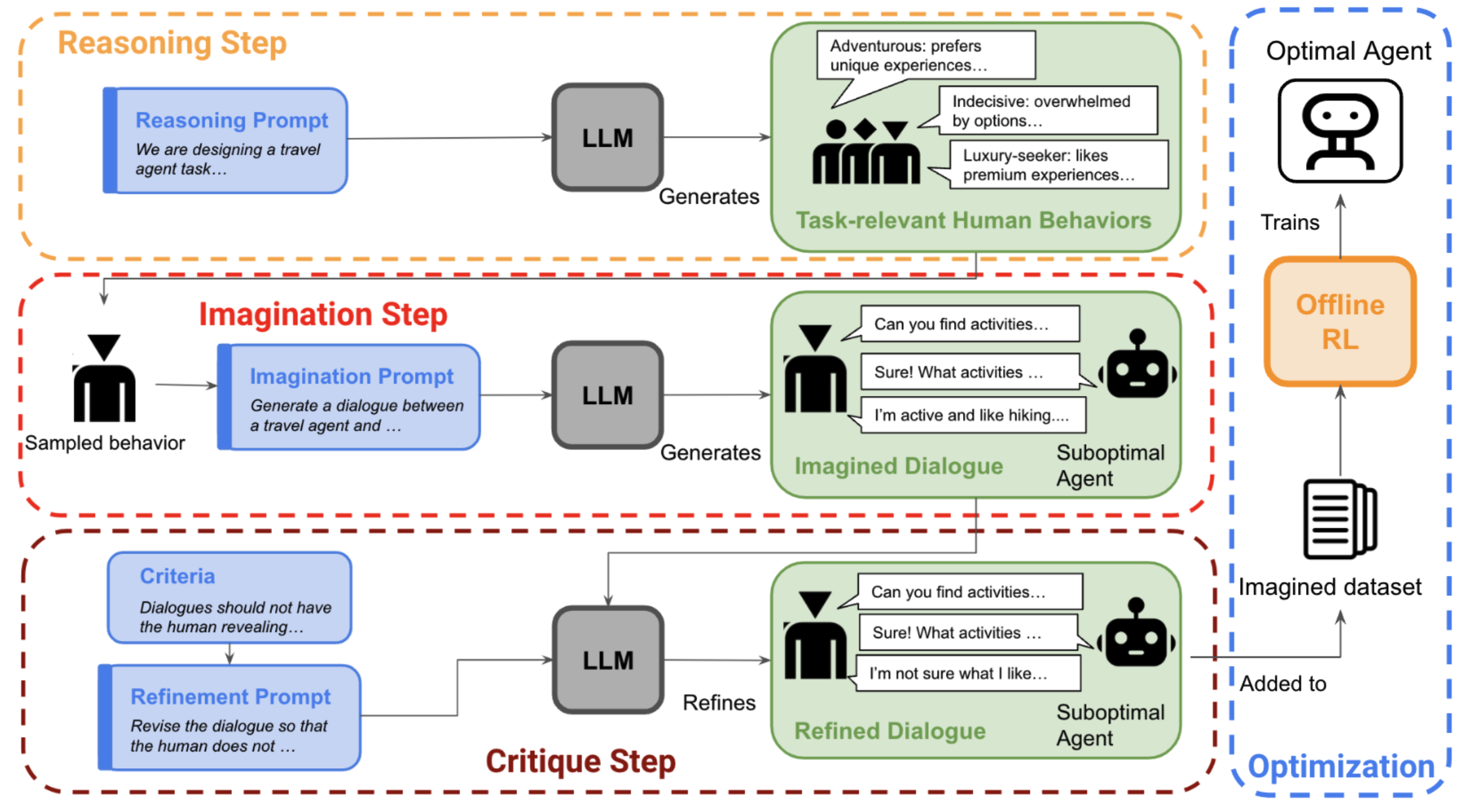
There are also works that curate benchmark datasets for training proactive querying. Andukuri et al. (2024) propose STaR-GATE, which teaches LMs to ask clarifying questions. They construct a dataset of under-specified user queries and train models to proactively elicit missing information before task completion, improving both question quality and task success rates. Zhou et al. (2025) introduce ColBench, a benchmark for evaluating multi-turn RL algorithms in realistic LLM agent scenarios, focusing on artifact creation tasks where agents must interact with simulated users to produce outputs like code, web pages, or slides that meet human expectations.

4. Future Directions

Querying During Chain-of-Thought Reasoning. Although finding EVOI-optimal queries is challenging, language models may still reason semantically about what to ask and how a query might improve its response.

Current language models can identify uncertainty during chain-of-thought reasoning, but they often make assumptions instead of proactively seeking clarification. For example, models like DeepSeek-R1 typically continue reasoning based on guesses rather than pausing to ask the user. The following is an example of such a conversation.

Prompt

Make a 3-day trip plan to Hawaii.

Response (DeepSeek-R1)

<think>

Okay, the user wants a 3-day trip plan to Hawaii. Let me start by figuring out which island they might be visiting. Hawaii has several main islands, like Oahu, Maui, Big Island, and Kauai. Since they didn’t specify, I should probably make a general plan that can be adapted. But maybe I should pick the most popular one for first-time visitors. Oahu is a common choice because it has Honolulu and Waikiki, Pearl Harbor, and the North Shore. That might be a good base.

…

We can encourage proactive querying behavior by modifying prompts. The following is a simple example.

Prompt

Make a 3-day trip plan to Hawaii.

Note: If any information is unclear or missing, stop thinking, ask the user for clarification before proceeding.

Response (DeepSeek-R1)

<think>

Okay, the user wants a 3-day trip plan to Hawaii. First, I need to figure out which island they’re interested in because Hawaii has several main islands like Oahu, Maui, Big Island, Kauai, etc. Each island has different attractions. Without knowing the specific island, the plan might be too generic or miss key spots. …

</think>

To create a tailored 3-day Hawaii itinerary, I need a few details:

1. Which island(s)?
   • Oahu, Maui, Big Island (Hawaii), Kauai, or multiple?
2. Interests:
   • Beaches, hiking, cultural/historical sites, adventure (e.g., snorkeling, surfing), food, or relaxation?
3. Transportation:
   • Will you rent a car, rely on tours, or use public transit?
4. Accommodation location:
   • Staying in one area (e.g., Waikiki, Lahaina, Kona) or moving around?
5. Budget:
   • Luxury, mid-range, or budget-friendly options?

Let me know, and I’ll craft a detailed plan! 🌺

ChatGPT Deep Research seems to consider a similar approach. Before proceeding to conduct the deep research, it always asks for clarification. This is reasonable as it takes a long time to conduct the deep research. The model does not want to waste time by making a wrong assumption.

Sampling-based EVOI Estimation. While computing EVOI directly is computationally expensive, we may still estimate it using sampling. This involves sampling candidate queries and possible user responses, then computing rewards for the resulting trajectories. There remains a trade-off between sample size and estimation accuracy.

Learning to Generate EVOI-Optimal Queries. Instead of explicitly computing EVOI, we can also train language models to learn good querying strategies using reinforcement learning, as in Hong et al. (2023). The agent sequentially poses queries and receives responses. When it believes it receives enough information, the agent generates a final response and receives a reward.

However, since insightful queries often require lookahead reasoning, it may be challenging to learn a general querying policy that works across tasks. Some form of EVOI-inspired inference-time optimization may still be necessary.

5. Related Work

There are several comprehensive surveys provide valuable insights into this field.

• There are other variations to represent reward uncertainty in MDPs, like MDP\R (Abbeel & Ng, 2004) and imprecise reward MDPs (Regan & Boutilier, 2010).
• Kaufmann et al. (2024) offer an extensive overview of RLHF.
• Weng (2024) discusses reward hacking, a significant challenge in learning reward functions within RLHF.
• The awesome-RLHF repository is an excellent resource for recent RLHF papers.
• For broader perspectives on AI safety and value alignment, readers may refer to earlier surveys (Amodei et al., 2016) (Leike et al., 2017).

6. Summary

This post explored user-specific alignment through proactive querying. We defined reward-uncertain MDPs as a foundation for modeling preference uncertainty, and showed how agents can select queries to reduce uncertainty (via entropy) or improve decision-making (via EVOI). While EVOI offers a principled objective, its computational challenges motivate practical approximations so that we can empirically compare it with existing querying strategies.

Citation

Cited as

Zhang, S. (Apr 2025). Towards Proactive Value Alignment. ReThink. https://shunzh.github.io/rethink/2025/04/10/alignment.html.

Or

@article{zhang2025towardsproactive,
  title   = "Towards Proactive Value Alignment",
  author  = "Shun Zhang",
  journal = "ReThink",
  year    = "2025",
  month   = "Apr",
  url     = "https://shunzh.github.io/rethink/2025/04/10/alignment.html"
}

References

1. Ouyang, L., Wu, J., Jiang, X., Almeida, D., Wainwright, C., Mishkin, P., Zhang, C., Agarwal, S., Slama, K., & Ray, A. (2022). Training Language Models to Follow Instructions with Human Feedback. Advances in Neural Information Processing Systems, 35, 27730–27744.
2. Sutton, R. S., & Barto, A. G. (2018). Reinforcement Learning: An Introduction. MIT Press.
3. Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., Van Den Driessche, G., Schrittwieser, J., Antonoglou, I., Panneershelvam, V., & Lanctot, M. (2016). Mastering the Game of Go with Deep Neural Networks and Tree Search. Nature, 529(7587), 484.
4. Schrittwieser, J., Antonoglou, I., Hubert, T., Simonyan, K., Sifre, L., Schmitt, S., Guez, A., Lockhart, E., Hassabis, D., Graepel, T., Lillicrap, T., & Silver, D. (2020). Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model. Nature, 588(7839), 604–609. https://doi.org/10.1038/s41586-020-03051-4
5. Ramachandran, D., & Amir, E. (2007). Bayesian Inverse Reinforcement Learning. International Joint Conference on Artificial Intelligence, 2586–2591.
6. Ng, A. Y., & Russell, S. (2000). Algorithms for Inverse Reinforcement Learning. Icml, 1, 2.
7. Ziebart, B. D., Maas, A. L., Bagnell, J. A., & Dey, A. K. (2008). Maximum Entropy Inverse Reinforcement Learning. Aaai, 8, 1433–1438.
8. Knox, W. B., & Stone, P. (2009). Interactively Shaping Agents via Human Reinforcement: The TAMER Framework. Proceedings of the Fifth International Conference on Knowledge Capture, 9–16.
9. Christiano, P. F., Leike, J., Brown, T., Martic, M., Legg, S., & Amodei, D. (2017). Deep Reinforcement Learning from Human Preferences. Advances in Neural Information Processing Systems, 4299–4307.
10. Zhang, S., Durfee, E. H., & Singh, S. (2017). Approximately-Optimal Queries for Planning in Reward-Uncertain Markov Decision Processes. Proceedings of the 27th International Conference on Automated Planning and Scheduling (ICAPS), 339–347.
11. Liang, X., Shu, K., Lee, K., & Abbeel, P. (2022). Reward Uncertainty for Exploration in Preference-based Reinforcement Learning (Number arXiv:2205.12401). arXiv.
12. Piriyakulkij, T., Kuleshov, V., & Ellis, K. (2023, November). Active Preference Inference Using Language Models and Probabilistic Reasoning. NeurIPS 2023 Foundation Models for Decision Making Workshop.
13. Viappiani, P., & Boutilier, C. (2010). Optimal Bayesian Recommendation Sets and Myopically Optimal Choice Query Sets. Advances in Neural Information Processing Systems (NIPS), 2352–2360.
14. Cohn, R., Singh, S., & Durfee, E. (2014). Characterizing EVOI-sufficient k-Response Query Sets in Decision Problems. Conference on Artificial Intelligence and Statistics, 131–139.
15. Kuhn, L., Gal, Y., & Farquhar, S. (2023). CLAM: Selective Clarification for Ambiguous Questions with Generative Language Models (Number arXiv:2212.07769). arXiv. https://doi.org/10.48550/arXiv.2212.07769
16. Li, B. Z., Tamkin, A., Goodman, N., & Andreas, J. (2023). Eliciting Human Preferences with Language Models (Number arXiv:2310.11589). arXiv. https://doi.org/10.48550/arXiv.2310.11589
17. Hong, J., Levine, S., & Dragan, A. (2023). Zero-Shot Goal-Directed Dialogue via RL on Imagined Conversations (Number arXiv:2311.05584). arXiv.
18. Andukuri, C., Fränken, J.-P., Gerstenberg, T., & Goodman, N. D. (2024). STaR-GATE: Teaching Language Models to Ask Clarifying Questions (Number arXiv:2403.19154). arXiv.
19. Zhou, Y., Jiang, S., Tian, Y., Weston, J., Levine, S., Sukhbaatar, S., & Li, X. (2025). SWEET-RL: Training Multi-Turn LLM Agents on Collaborative Reasoning Tasks (Number arXiv:2503.15478). arXiv. https://doi.org/10.48550/arXiv.2503.15478
20. Abbeel, P., & Ng, A. Y. (2004). Apprenticeship Learning via Inverse Reinforcement Learning. Proceedings of the Twenty-First International Conference on Machine Learning, 1–8.
21. Regan, K., & Boutilier, C. (2010). Robust Policy Computation in Reward-Uncertain MDPs Using Nondominated Policies. Assoc. for Adv. of Artificial Intelligence (AAAI), 1127–1133.
22. Kaufmann, T., Weng, P., Bengs, V., & Hüllermeier, E. (2024). A Survey of Reinforcement Learning from Human Feedback (Number arXiv:2312.14925). arXiv. https://doi.org/10.48550/arXiv.2312.14925
23. Weng, L. (2024). Reward Hacking in Reinforcement Learning. https://lilianweng.github.io/posts/2024-11-28-reward-hacking/.
24. Amodei, D., Olah, C., Steinhardt, J., Christiano, P., Schulman, J., & Mané, D. (2016). Concrete Problems in AI Safety. ArXiv Preprint ArXiv:1606.06565.
25. Leike, J., Martic, M., Krakovna, V., Ortega, P. A., Everitt, T., Lefrancq, A., Orseau, L., & Legg, S. (2017). AI Safety Gridworlds. ArXiv Preprint ArXiv:1711.09883.